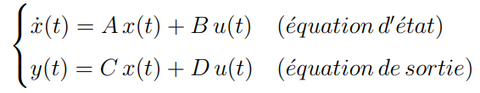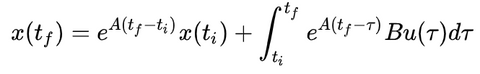Systèmes Mono Variables
Etats Mono Variable
Un système mono variable est décrit en fonction de son état, dépendant de son unique entrées « u » et de son unique sortie « y » mais aussi en fonction de son comportement dynamique interne.
Le plus petit ensemble, de « n » variables d’état {x1, x2 …xn}, à un instant t>0 (système causal), définit l’état du système (connu aussi pour T0=0). C’est un ordre « n »
Cet ensemble de « n » variables d’état {x1, x2 …xn} défini le vecteur d’état x(x1, x2 …xn)T, qui évolue dans un espace d’état, ce qui en constitue une modélisation.
Le plus petit ensemble, de « n » variables d’état {x1, x2 …xn}, à un instant t>0 (système causal), définit l’état du système (connu aussi pour T0=0). C’est un ordre « n »
Cet ensemble de « n » variables d’état {x1, x2 …xn} défini le vecteur d’état x(x1, x2 …xn)T, qui évolue dans un espace d’état, ce qui en constitue une modélisation.
Equation différentielle Mono Variable
Un système de 1 variable de sorties avec « n » variables d’état possède un modèle mathématique basé sur un système de 1 équations différentielles de degré « n »:
Equation Matricielle Mono Variable
Le système d'équations peut s'écrire sous forme matricielle: A.Y = B.U
Modèle d'Etat Linéaire Invariant
Un modèle d’état, d’entrée « u » et de sortie « y », avec un état « x », linéaire et invariant (stationnaire), est représenté par un système à 2 équations ou des termes « A », « B », « C » et « D » sont des matrices d’état (Ann), de commande (Bnm), de sortie (Cpn) et de transmission (Dpm).
Calcul du Temps Final
L’état du système est un résumé exhaustif du passé, et connaissant un temps initial (ti) on peut calculer l’état à un temps final (tf) grâce à l’intégration de l’équation d’état :
Schéma Bloc
La représentation synoptique du modèle d’état est alors le schéma bloc suivant :
