Impédances

Définition

L'impédance électrique mesure l'opposition d'un circuit électrique au passage d'un courant alternatif sinusoïdal. La définition de l'impédance est une généralisation de la loi d'Ohm au courant alternatif:

• Formule: U = Z . I
• Unité: Ohm (Ω).

Le concept d'impédance permet d'appliquer au régime sinusoïdal les formules utilisées en régime continu, tout en intégrant l'effet d'éléments capacitifs et inductifs.

Le mot impédance fut inventé par Oliver Heaviside en juillet 1886. Il vient du verbe anglais to impede signifiant « retenir », « faire obstacle à » ; verbe qui dérive lui-même du latin impedire qui veut dire « entraver ».

Déphasage

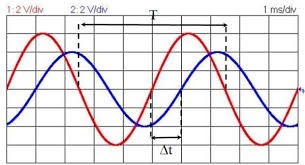
En régime sinusoïdal il existe un décalage de temps (Δt) entre la tension et l'intensité. Ramené en notion d'angle, on parle de déphasage:

• Formule: ɸ = 2π . (Δt / T)
• Formule: ɸ = 360° . (Δt / T)
• Unités: Radian ou degrés.

On utilise aussi les fonctions trigonométriques associées: sinus(ɸ), cosinus(ɸ) ou tangente(ɸ).

Triangle des impédances

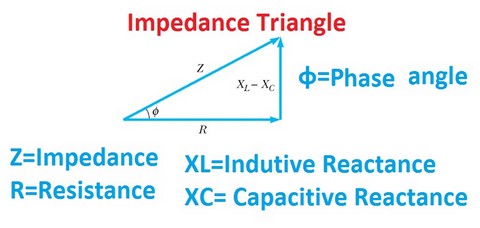
Le déphasage (ɸ) entre tension et intensité, est lié aux réactances (induction et capacité) du dipole:

• R: résistance
• X: réactance (inductive XL et capacitive XC).
• Z: impédance.

On défini ainsi un triangle rectangle de cotés résistance et réactance et d'hypothénuse impédance.

Impédances de base

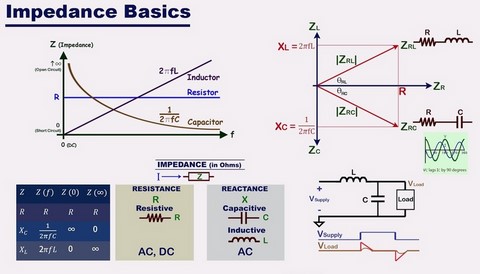
Les impédances sont facteurs des caractérisque du dipole (résistance R, induction L, capacité C) et des caractéristique du signe (fréquence f, période T, avec f=1/T):

• résistance pure (ohm): ZR = R.
• induction pure: ZL = L . (2π.f).
• capacité pure: ZC=  1 / [ C. (2π.f) ].

On défini aussi la pulsation: ώ = (2π.f).

Impédances Complexes

Le triangle des impédances est raporté sur un repère orthonormé, associé au plan des complexes:

• abscisses (x): partie réelle (résistances).
• ordonnées (y): partie imaginaire (réactances).
• impédance complexe: Z = (R) + i . (XL + XC)

A noter qu'on remplace souvent le symbole "i"" mathématique par le symbole "j" électrique.