Séries de FOURIER
Concept de base
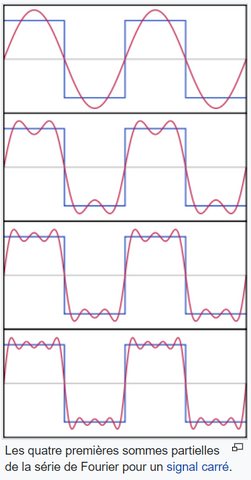
Tout signal périodique (de fréquence f) de forme quelconque, peut être obtenu en ajoutant à une sinusoïde de la même fréquence (fondamentale f), des sinusoïdes dont les fréquences sont des multiples entiers (harmoniques) de cette fréquence f, ces signaux (harmoniques) ayant des amplitudes et des positions de phase appropriées.
Les domaines d'applications sont multiples:
• Physique: tout signal périodique de fréquence initiale est du à la superposition de signaux de fréquences multiples. Réciproquement, toute superposition de signaux de fréquences multiples engendre un signal de la fréquence initiale.
• Mathématiques: tout polynome trigonométrique P(x) peut s'écrire comme une somme infinie (∑) d'expressions exponentielles (e2п.i.x) correspondant à des fonctions trigonométriques (en notation d'EULER).
Les études en mathématiques fondamentales aboutissent à des outils appliqués aux diverses sciences physiques, telles que l'électricité, la mécanique, l'optique, la thermodynamique ...
Forme exponentielle complexe
En analyse mathématique, les séries de FOURIER sont un outil fondamental dans l'étude des fonctions périodiques. C'est à partir de ce concept que s'est développée la branche des mathématiques connue sous le nom d'analyse harmonique:
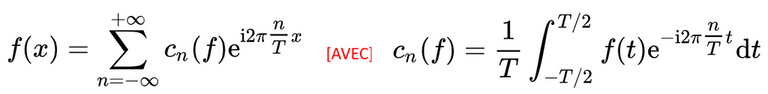
Forme trigonométrique réelle
Tout signal à temps continu s(t) périodique, de période To (et de pulsation ω0 = 2п/T0), peut s’écrire sous la forme d'une valeur moyenne a0 et de la somme de signaux harmoniques, de rang 1 à n:
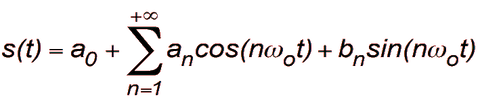
Spectres
Les spectres d'amplitude et de phase sont des graphique permettant de visualiser les valeurs des harmoniques de rang n, en amplitudes, soit An=√(an²+bn²), et en phases, soit φn=arctan(bn/an), en fonction des fréquences de pulsation ω=2π/f:

Identité de PARSEVAL
Pour des signaux périodiques, à énergie infinie mais à puissance moyenne finie, l'identité de PARSEVAL montre l’égalité du calcul de la puissance moyenne d’un signal périodique de période To à partir de sa représentation dans le domaine temporel ou fréquentiel:
