Quadripoles Passifs
Fonction de transfert
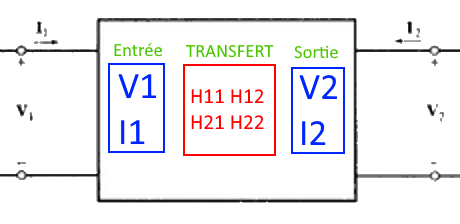
La fonction de transfert H(1,2, ...) permet de relier les caractéristiques d'entrée (V1, I1, ...) aux caractéristiques de sortie (V2, I2, ...). Son expression est fonction des espaces considérés:
• Temporel: H(t) = S(t) / E/(t).
• Fourier: H(jω) = S(jω) / E(jω).
• Laplace: H(p) = S(p) / E(p).
On étudie en général les réponses dans le temps pour des variations de fréquences (Fourier) ou différents types de signaux test (Laplace).
Réponse fréquencielle
La réponse fréquencielle étudie le signal de sortie pour un signal d'entrée de fréquence variable:
• Fourier: H(f) = S(f) / E(f).

Réponse indicielle
La réponse indicielle étudie le signal de sortie pour un signal d'entrée de type spécifique (signal test):
• Laplace: H(p) = S(p) / E(p).
• Laplace: H(p) = S(p) / E(p).
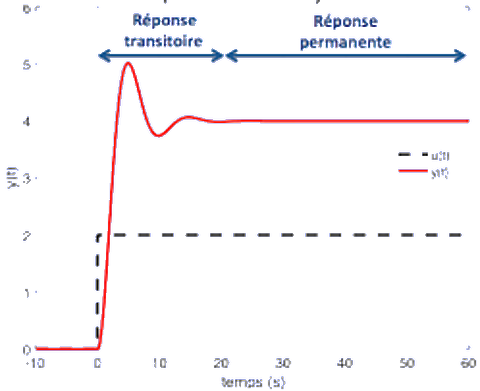
Systémes linéaires
En pratique, du fait des saturations, hystérésis ou autres, aucun système n'est linéaire. Toutefois, un système pourra être considéré parfois comme linéaire dans certaines plages d'utilisation. Dans ces cas là, il est régi par un système d'équations différentielles linéaires, sur la plage concernée.
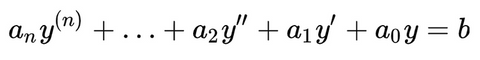
Systémes linéaires (premier ordre)
Un système linéaire du premier ordre est régi par une équation différentielle limitée à une dérivée première:
• Equation différentielle générale: a1.y(1) + a0.y = b
• Caractéristiques: constante de temps (τ) et gain statique (K)
• Equation différentielle réduite: τ.y(1) + y = K . x
• Fonction de Transfert: H(s) = K / (1+τ.s)
• Solution: y(x) = Y0 . e-A.x.
• Solution: y(x) = Y0 . e-A.x.
• Solution: y(t) = (K/τ) . e-t./τ
Les caractéristiques indicielles et fréquentielles sont les suivantes:
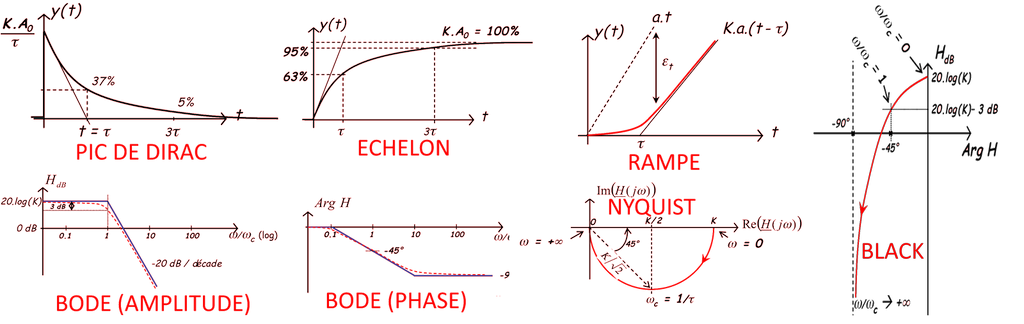
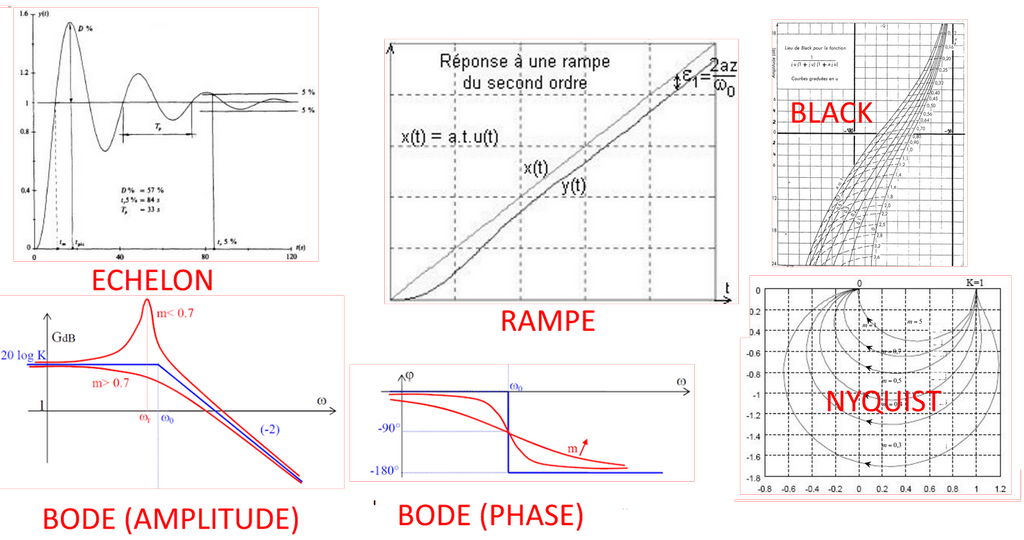
Systémes linéaires (second ordre)
Un système linéaire du second ordre est régi par une équation différentielle limitée à une dérivée seconde:
• Equation différentielle générale: a2.y(2) + a1.y(1) + a0.y = b
• Caractéristiques: pulsation propre (ω0), amortissement (m) et gain statique (K)
• Equation différentielle réduite: y(2) + 2.m.ω0 .y(1) + ω02.y = K.ω02 . x
• Fonction de Transfert: H(s) = K / (1 + 2m/ω0. . s + s2/ω02)
• Solution: y(x) = ... (suivant les valeurs de m).
• Solution: y(x) = ... (suivant les valeurs de m).
• Solution: y(t) = ... (suivant les valeurs de m).
Les caractéristiques indicielles et fréquentielles sont les suivantes: