Puissances
Puissances Electriques
La puissance électrique que l'on note souvent P et qui a pour unité le Watt (symbole W) est le produit de la tension électrique aux bornes de laquelle est branchée l'appareil (en Volts) et de l'intensité du courant électrique qui le traverse (en Ampères) pour des appareils purement résistifs [Wikipédia].
En Courant Continu (CC) ou en Courant Alternatif (CA) Monophasé (MONO):
• P=U.I.cos(φ) : puissance active, exprimée en Watt (W);
• P=U.I: lorsque le cos(φ) vaut "1", en Courant Continu (CC) ou pour des circuits purement résistifs;
En régime alternatif, triphasé (TRI) sans neutre, ou triphasé avec neute (TETRA), les puissances sont de 3 ordres:
• P=U.I: lorsque le cos(φ) vaut "1", en Courant Continu (CC) ou pour des circuits purement résistifs;
• P=U.I.√3.cos(φ): puissance active, exprimée en Watt (W);
• Q=U.I.√3.sin(φ): puissance réactive, exprimée en Volt Ampéres Réactif (VAR);
• S=U.I.√3: puissance apparente, exprimée en Volt Ampère (VA);
• Q=U.I.√3.sin(φ): puissance réactive, exprimée en Volt Ampéres Réactif (VAR);
• S=U.I.√3: puissance apparente, exprimée en Volt Ampère (VA);
Intensités
L'Intensité Nominale In(A) se calcule directement à partir de la puissance électrique nominale Pn(W):
• In=Pn/U/cos(φ): en réseau monophasé (MONO);• In=Pn/U/√3/cos(φ): en réseau triphasé sans neutre (TRI), ou triphasé avec neutre (TETRA);
Conformément à la norme NF C 15.100, le courant d'emploi Ib est issu du courant nominal In, après application de 3 facteurs:
• ku: facteur d'utilisation. Il caractérise le taux d'utilisation de la charge en fonction du temps.• kf: facteur de simultanéité. Il caractérise les conditions d'exploitation de l'installation notamment pour les moteurs et les prises de courant.
• ke: facteur d'évolution. Il permet de prendre en compte les évolutions prévisible de l'installation.
L'Inténsité de Réglage (Ir) est celle du calibre normalisé imédiatement supérieur:
230V Cos=0,8 | 1A | 1,6A | 2A | 3A | 4A | 5A | 6A | 8A | ||
|---|---|---|---|---|---|---|---|---|---|---|
0.18kW | 0,29kW | 0,37kW | 0,55kW | 0,74kW | 0,92kW | 1,10kW | 1,47kW | |||
10A | 12A | 16A | 20A | 25A | 32A | 40A | 50A | 63A | 80A | |
1,8kW | 2,2kW | 2,9kW | 3,7kW | 4,6kW | 5,9kW | 7,4kW | 9,2kW | 11,6kW | 14,7kW | |
100A | 125A | 160A | 200A | 250A | 320A | 400A | 500A | 600A | 800A | |
18kW | 22kW | 29kW | 37kW | 46kW | 59kW | 74kW | 92kW | 116kW | 147kW | |
400V Cos=0,8 | 1A | 1,6A | 2A | 3A | 4A | 5A | 6A | 8A | ||
0,32kW | 0,51kW | 0,64kW | 0,96kW | 1,28kW | 1,60kW | 1,92kW | 2,56kW | |||
10A | 12A | 16A | 20A | 25A | 32A | 40A | 50A | 63A | 80A | |
3,2kW | 3,8kW | 5,1kW | 6,4kW | 8,0kW | 10,2kW | 12,8kW | 16,0kW | 19,2kW | 25,6kW | |
100A | 125A | 160A | 200A | 250A | 320A | 400A | 500A | 630A | 800A | |
32kW | 40kW | 51kW | 64kW | 80kW | 102kW | 128kW | 160kW | 192kW | 256kW | |
1000A | 1250A | 1600A | 2000A | 2500A | 3200A | |||||
320kW | 400kW | 512kW | 640kW | 800kW | 1.024kW |
Diagramme complexe
La représentation de FRESNEL est un outil graphique permettant d'ajouter, de soustraire, de dériver et d'intégrer des fonctions sinusoïdales de même fréquence.
À toute grandeur fonction sinusoïdale du temps on fait correspondre un vecteur. En électricité, l’amplitude vaut (UI) et l’angle polaire est égal à la phase (φ).
Somme vectorielle
La somme de 2 vecteur A(a,α) et B(b,β) est un vecteur (A+B) de norme fonction des normes (a) et (b) et phase fonction des phases (α) et (β).
L’abscisse de la somme est égale à la somme des abscisses, idem pour les ordonnées (règle du parallélogramme):
x(A+B) = x(A) + x(B)
y(A+B) = y(A) + y(B)
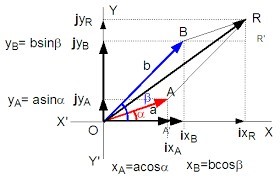
Compte tenu des expression des normes et phases en fonction des coordonnées, il reste:
|A+B| = √ ( [a.cos (α) + b.cos(β)]² + [a.sin (α) + b.sin(β)]² )
Méthode
La méthode de BOUCHEROT permet, en régime sinusoïdal de tension et de courant, de calculer la puissance totale consommée par une installation électrique comportant plusieurs dipôles électriques de facteur de puissance divers, ainsi que l'intensité totale appelée:
• PT = ∑Pi : la puissance active totale est égale à la somme des toutes les puissances actives unitaires;• QT = ∑Qi : la puissance réactive totale est égale à la somme des toutes les puissances réactives unitaires;
Cette méthode mise au point par Paul BOUCHEROT, permet de faire des calculs selon un formalisme de type vectoriel sans utiliser la représentation de FRESNEL trop lourde lorsque l'on est en présence de nombreux dipôles [Wikipédia].
C'est une méthode issue des calculs vectoriels (sans utilisation de la méthode par représentation de FRESNEL): |u+v| = √ ( (ux + vx)² + (uy + vy)² )
ou encore: |u+v| = √ ( (|u|.cos(u) + |v|.cos(v) )² + ( |u|.sin(u) + |v|.sin(v) )² )
VECTEURS (v) PUISSANCES | |v| . cos(v) UI . cos(PHI) | |v| . sin(v) UI . sin(PHI) | |v| UI |
|---|---|---|---|
v1 | |v1| . cos(v1) | |v1| . sin(v1) | |v1| |
v2 | |v2| . cos(v2) | |v2| . sin(v2) | |v2| |
v3 | |v3| . cos(v3) | |v3| . sin(v3) | |v3| |
. . . | . . . | . . . | . . . |
vn | |vn| . cos(vn) | |vn| . sin(vn) | |vn| |
TOTAL | X = ∑ ( |vi| . cos(vi) )² | Y = ∑ ( |vi| . sin(vi) )² | √ ( ∑ (X2 + Y2) ) |
SOMMES VECTORIELLES | |||
Mise en oeuvre
Une Base De Données répertorie les consommateurs, chaque enregistement correspondant à une ligne électrique (protection):
• P(kW): en général, la puissance active (kW) est donnée par le fabricant (ou indirectement par son COS).• Q(kVAR): souvent calculée à partir du facteur de puissance (COS).
• S(kVA): directement issue de la caractèristique de la ligne (U, I).La puissance apparente totale est : STOT = √(∑Pi² + ∑Qi² )
Ceci permet de définir alors le facteur de puissance général de l'installation.
NUM | UTILISATION | Pn(kW) | Un(V) | COS | RESEAU | In(A) | ku | ks | ke | Ib | Ir | I% | P(kW) | Q(kVAR) | S(kVA) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
Q01 | ECLAIRAGE: ECL 1x45W ECL 1x60W ECL 1x75W ECL 1x100W | 0,280 (0,045) (0,060) (0,075) (0,100) | 230 | 0,8 | MONO | 1,5 | 1,00 | 1,00 | 1,20 | 1,80 | 10 | 82% | 0,336 | 0,252 | 0.420 |
Q02 | PRISES: 8x1000W | 8,000 (8,000) | 230 | 0,8 | MONO | 43,5 | 1,00 | 0,21 | 1,20 | 11,1 | 16 | 31% | 2,040 | 1,530 | 2,550 |
Q03 | CHAUFFAGE: 1x2000W 1x2500W | 4,500 (2,000) (2,500) | 230 | 1,0 | MONO | 19,6 | 1,00 | 1,00 | 1,00 | 19,6 | 20 | 2% | 4,500 | 0,000 | 4,500 |
Q04 | FOUR: 1x4600W | 4,600 (4,600) | 230 | 1,0 | MONO | 17,4 | 1,00 | 1,00 | 1,00 | 17,4 | 20 | 13% | 4,000 | 0,000 | 4,000 |
Q05 | MOTEUR 01: 1x18kW | 18 | 400 | 0,8 | TRI | 32,5 | 1,00 | 1,00 | 1,20 | 39,0 | 40 | 3% | 21,600 | 16,200 | 27,000 |
Q06 | MOTEUR 02: 1x9kW | 9 | 400 | 0,8 | TRI | 16,2 | 1,00 | 0,75 | 1,20 | 14,6 | 16 | 9% | 8,900 | 6,075 | 10,125 |
Q07 | MOTEUR 03: 1x2,2kW | 2,2 | 400 | 0,8 | TRI | 4,0 | 1,00 | 0,60 | 1,20 | 2,9 | 4 | 29% | 1,584 | 1,188 | 1,980 |
Q00 | TOTAL | 55kW | 400V | 0,86 | TETRA | 92A | 1,00 | 0,89 | 1,00 | 71A | 80A | 11% | 42kW | 25kVA | 49kVA |
Exemple pratique
Le bilan de puissance est fait par tableaux électriques, chacun détaillant l’exhaustivité des protections (disjoncteurs, fusibles, …) câblées (utilisées ou en Réserve Equipée).
Des liaisons peuvent être fait entre fiches de cacul en fonction de l’’architecture du réseau électrique.
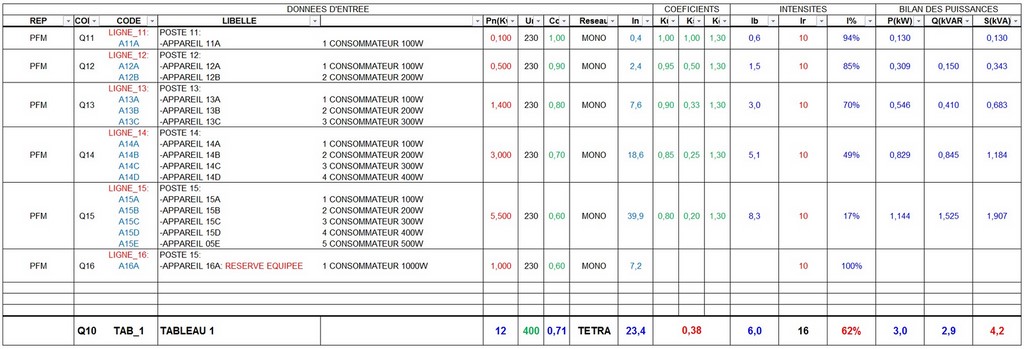
Retour d'expérience (REX)
Le choix des coéficients permettant de passer du courant nominal (In) au courant d'emploi (Ib) est donc primordial, fonction de l'architecture du réseau et des coéficients associés, avec prises de risques:
• sur-estimation: sans pendre de risques, donc avec des valeurs toutes proches de 1, le total monte vite. Les incidences techniques et financiéres sont significatives (effet cascade).• sous-estimation: avec prises de risques, soit avec des valeurs faibles, il faut toujours vérifier que le calibre nominal permette le passage des pointes passagères (démarrages et autres aléas).
