MAINT-FAIL: Défaillances
Défaillances
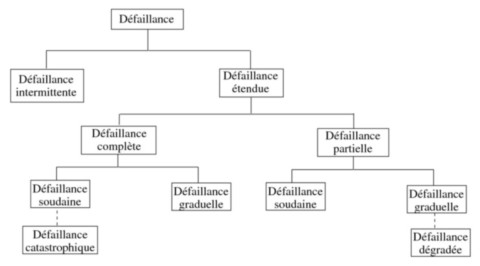
Le passage de l'état de FONCTIONNEMENT à l'état de PANNE constitue une transition appelée DEFAILLANCE. Plusieurs définitions ou synonymes selon la norme AFNOR X 60-011:
• DEFAILLANCE: « altération ou cessation d’un bien à accomplir une fonction requise ».
• DEFAILLANCE PARTIELLE: altération du fonctionnement.
• DEFAILLANCE COMPLETE: cessation du fonctionnement (panne).
• DEFAILLANCE CATALECTIQUE: soudaine et complète.
• DEFAILLANCE PAR DEGRADATION: progressive et partielle.
• DEFAILLANCE ALEATOIRE: taux de défaillance constant.
• DEFAILLANCE USURE: taux de défaillance croissant.
Il existe assi des synonymes (non normalisés), comme « faillures » (pour dommages, dégâts, anomalies,avaries, incidents, défauts, pannes) utilisés dans divers métiers.
Indicateur
Pour suivre cette défaillance, on mesure la disponibilité (D%), inverse du taux de défaillance (λ) . Elle varie de 0% (en cas de panne) à 100% (en fonctionnement), mais fluctue dans le temps:
• jeunesse: taux de défaillance (λ) élevé, puis décroissant.
• vie utile: taux de défaillance (λ) stable.
• vieillesse: taux de défaillance (λ) croissant pour redevenir élevé.
• vie utile: taux de défaillance (λ) stable.
• vieillesse: taux de défaillance (λ) croissant pour redevenir élevé.
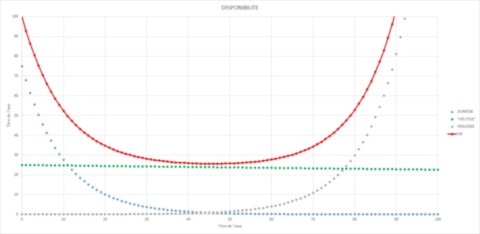
La courbe de disponibilité globale est la somme des disponibilités pendant ces 3 périodes: elle présente une allure en forme dite de « baignoire ».
Comme pour la vie humaine, la disponibilité est de 100% au début, puis décroit pendant une période de jeunesse pour se stabiliser pendant la vie utile. Ensuite, la vieillesse intervient avec des défaillances de plus en plus nombres.
Modéles mathématiques
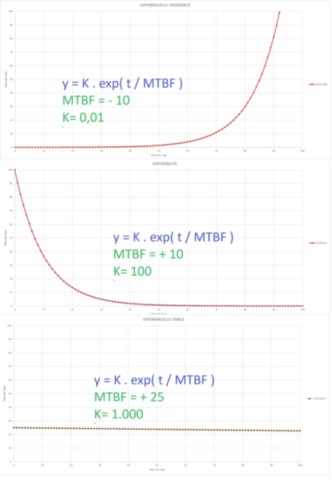
Une modélisation mathématique est possible avec la fonction EXPONENTIELLE de variable (t) et de paramètre (MTBF), avec modulation d'amplitude (K), soit une courbe d'équation K . e( t / MTBF), différentes allures reconnaissables suivants les valeurs des paramètres:
• croissance: MTBFc = -10 Kc = 0,01.
• décroissance: MTBFd = +10 Kd = 100.
• décroissance: MTBFd = +10 Kd = 100.
• stabilité: MTBFs = 1000 Ks = 25.
Le coefficient de modulation d'amplitude (K) peut aussi être intégré dans la valeur de l'exponentielle, soit e( [t / MTBF] + K'). C'est l'exponencielle d'une droite, de pente λ=1/MTBF et d'abcisse à l'origine D=ln(K):
• croissance: λc = -0,1 Dc = 4,605.
• stabilité: λs = 0,1000 Ds = 4,605.
• décroissance: λd = +0,1 Dd = 4,605.
• stabilité: λs = 0,1000 Ds = 4,605.
• décroissance: λd = +0,1 Dd = 4,605.
La courbe finale est la sommes des courbes élémentaires (principe de superposition) des parties croissance (c), stabilité (s) et décroissance (d), chacune avec leurs propres paramètres MTBF (ou λ=1/MTBF) et K (ou D=lnK).
Avec un bon paramètrage, on retrouve effectivement une courbe globale de type « baignoire », par exemple:
• Temps: de T0 = 0 à T100 = 100
• MTBF: croissance à -10 (donc -10%), décroissance à +10 (donc +10%), stabilité à +1.000 (donc x10)
• amplitude: croissance à 0,01 décroissance à 100, stabilité croissance: 25.
• MTBF: croissance à -10 (donc -10%), décroissance à +10 (donc +10%), stabilité à +1.000 (donc x10)
• amplitude: croissance à 0,01 décroissance à 100, stabilité croissance: 25.
Loi géométrique
La probabilité de défaillance (avant un temps t) utilise une loi géométrique et une loi exponentielle ou µ représente le temps moyen de fonctionnement avant une panne (MTTF), le taux de défaillance étant l’inverse (λ = 1/µ). Ce taux moyen de défaillance λ, probabilité de défaillance par unité de temps, est supposé constant.
La fonction de répartition de la probabilité d’une défaillance dans les k premières années, part du principe que la probabilité conditionnelle d'une panne dans l’année k+1 (avec un fonctionnement de k années), sera la même que la probabilité d’une défaillance dans l’année k (avec un fonctionnement de k-1 années), processus sans mémoire.
La probabilité de défaillance (par année) est p = λ et la probabilité de non panne (par année) est q = 1 - λ, et la probabilité d’une première défaillance dans l’année k est P(X=k).
La probabilité de défaillance (par année) est p = λ et la probabilité de non panne (par année) est q = 1 - λ, et la probabilité d’une première défaillance dans l’année k est P(X=k).
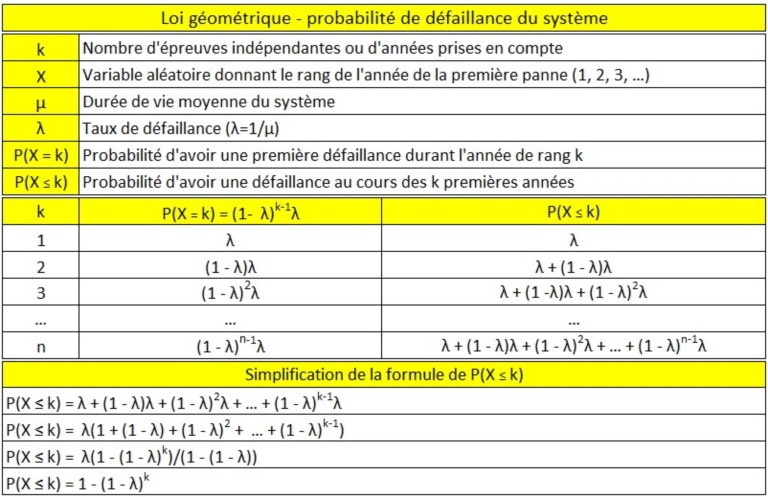
La variable X suit une loi géométrique où X représente le « nombre d’épreuves de Bernoulli », indépendantes de probabilité de panne nécessaire pour obtenir la première défaillance. La probabilité d’avoir une première panne durant la kième année est P(X=k) = (1 - p)k-1p avec λ=p, soit: P(X=k) = (1 - λ)k-1λ
La probabilité de défaillance des k premières années est: P(X ≤ k) = P(X=1) + P(X=2) + ... + P(X=K).
La probabilité de défaillance des k premières années est: P(X ≤ k) = P(X=1) + P(X=2) + ... + P(X=K).
Soit: P(X ≤ k) = λ + (1 - λ) . λ + ... + (1 - λ) . (k-1) . λ
C'est une suite arithmétique de raison (1 - λ) et de premier terme 1: P(X ≤ k) = 1 - (1 - λ)k
C'est une suite arithmétique de raison (1 - λ) et de premier terme 1: P(X ≤ k) = 1 - (1 - λ)k
Loi exponentielle
En divisant le temps en n intervalles réguliers, le taux moyen de défaillance λn est proche de λ/n et la formule devient: P(X ≤ k) ≈ 1 - (1 - λ/n)k
Avec un changement de variable en T=X/n, la probabilité P(T<t) est un calcul de limite lorsque n tends vers l'infini ...
Ce calcul de limite permet de déduire: P(T<t) ≈ 1 - (e-λ)t
C'est l'expression classique de la probabilité d'avoir une défaillance sur l'intervalle de temps [0,t], la probabilité de ne pas avoir de défaillance étant le complément, soit: (e-λ)t
Fiabilité d'une chaine
Une chaine est composée de maillons: ce qui fait la force de la chaine, c'est la résistance de son maillon le plus faible. Ces maillons sont montés en série, les uns apres les autres. Mais pour renforcer la résistance, plusieurs chaines peuvent être montées en parrallele ...
Il en va de même pour équipement qui est constitué de (n) composants possédant chacun son propre taux de défaillance unitaire (D%i ).
Dans un montage en série, pour que le système fonctionne il faut que tous les constituants fonctionnent, le taux de défaillance total (D%TOT) est le produit des taux de défaillances unitaires (D%i):
• D%TOT = ∏in D%i
Dans un montage parralléle, pour que le système fonctionne il faut qu'au moins un constituant fonctionnent, le taux de fonctionnement total (1 - D%TOT) est le produit des taux de fonctionnements unitaires (1 - D%i):
• (1 - D%TOT) = ∏in (1 - D%i)
Pour augmenter la Sécurité de Fonctionnement (SF) on utilise des chaines en parrallèle pour assurer une même fonction.
• (1 - D%TOT) = ∏in (1 - D%i)
Pour augmenter la Sécurité de Fonctionnement (SF) on utilise des chaines en parrallèle pour assurer une même fonction.
En résumé ...
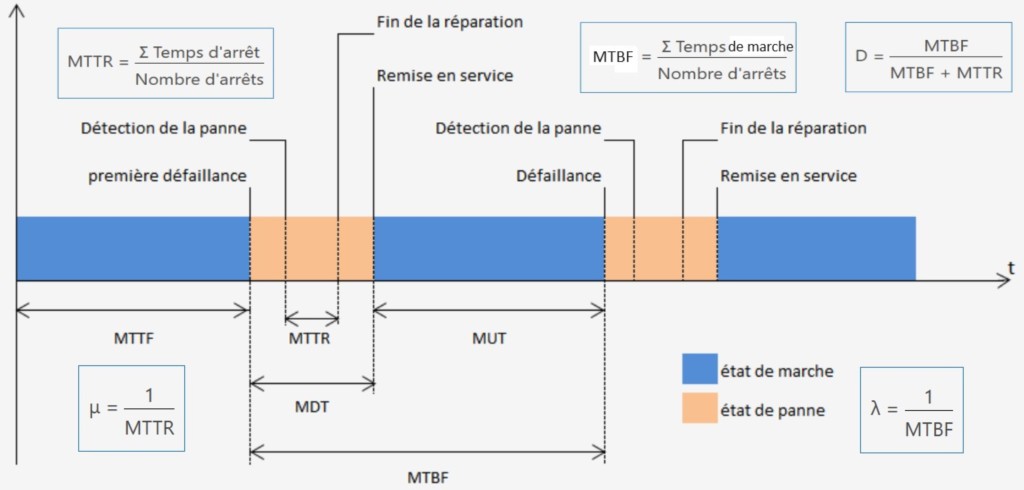
Les indicateurs principaux sont des temps moyens de marche (MTBF) et d'arrêt (MTTR) par rapport aux nombres d'arrêt. D'autres indicateurs en découlent, comme la disponibilité (D%) et des paramêtres fondamentaux, tels que le taux de défaillance (λ) et le taux de réparation (µ):
• MTBF = TEMPSARRET / NOMBREARRET
• MTTR = TEMPSMARCHE / NOMBREARRET
• MTTR = TEMPSMARCHE / NOMBREARRET
• D% = MTBF / (MTBF + MTTR)
• λ = 1 / MTBF
• λ = 1 / MTBF
• µ = 1 / MTTR
Rappelons que toutes ces analyses reposent sur des calculs de probabilités ...