Transformation de FOURIER
Expression mathématique
En mathématiques, la Transformation de FOURIER est une transformation intégrale, associant à une fonction ƒ(ω) (sur les réels positifs ω) une nouvelle fonction F(f) dite Transformée de Fourier (sur les réels f):
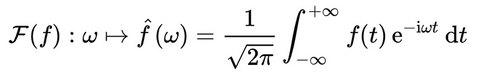
Propriétés
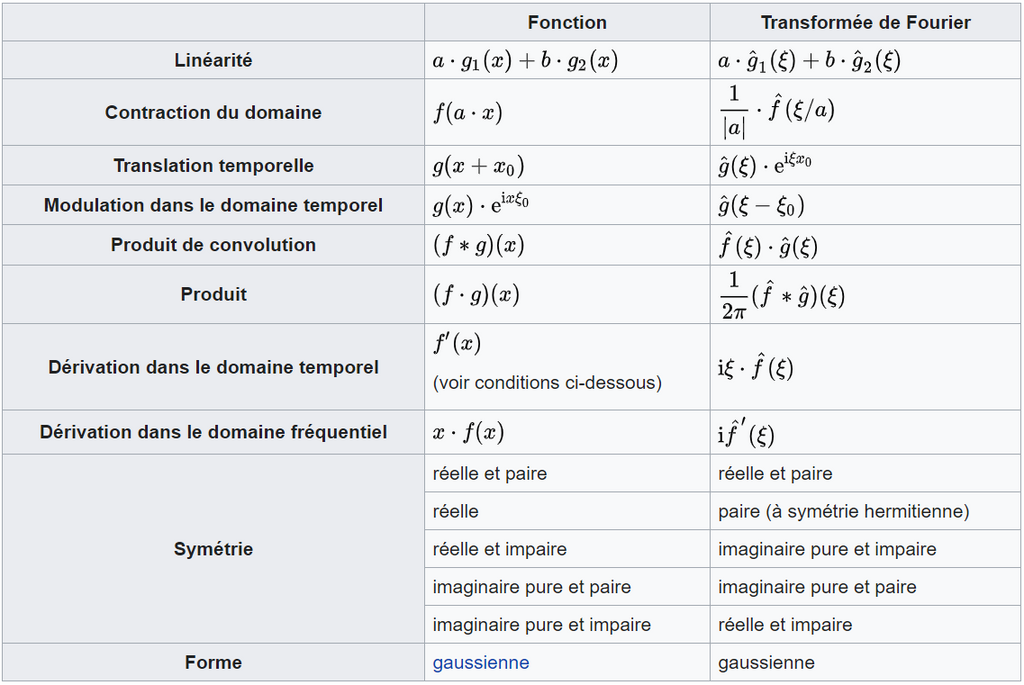
Les propriétés de la Transformation de FOURIER seront utilisées pour résoudre des équations linéaires (en f) issues d'équations différentielles (en t):
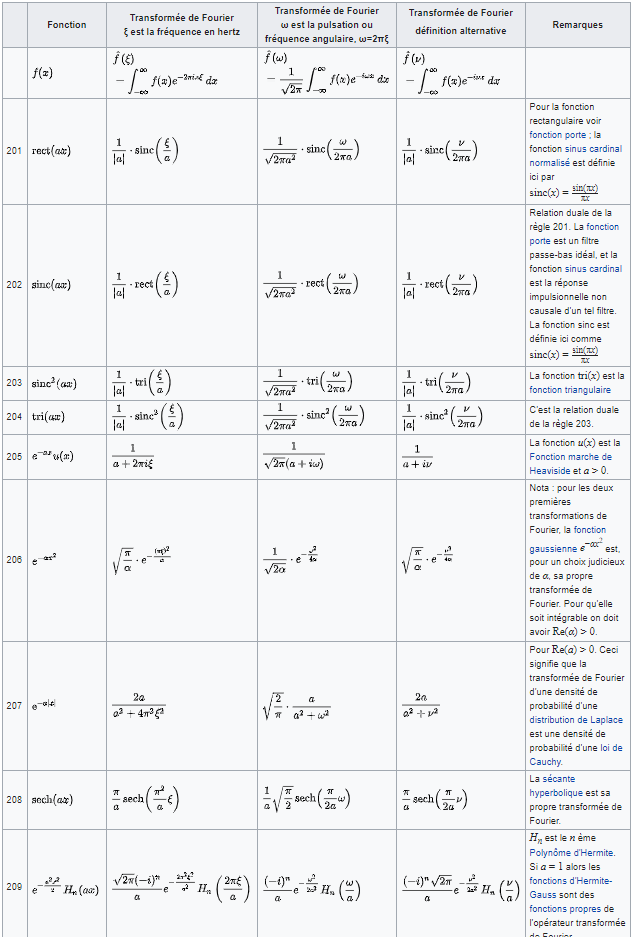
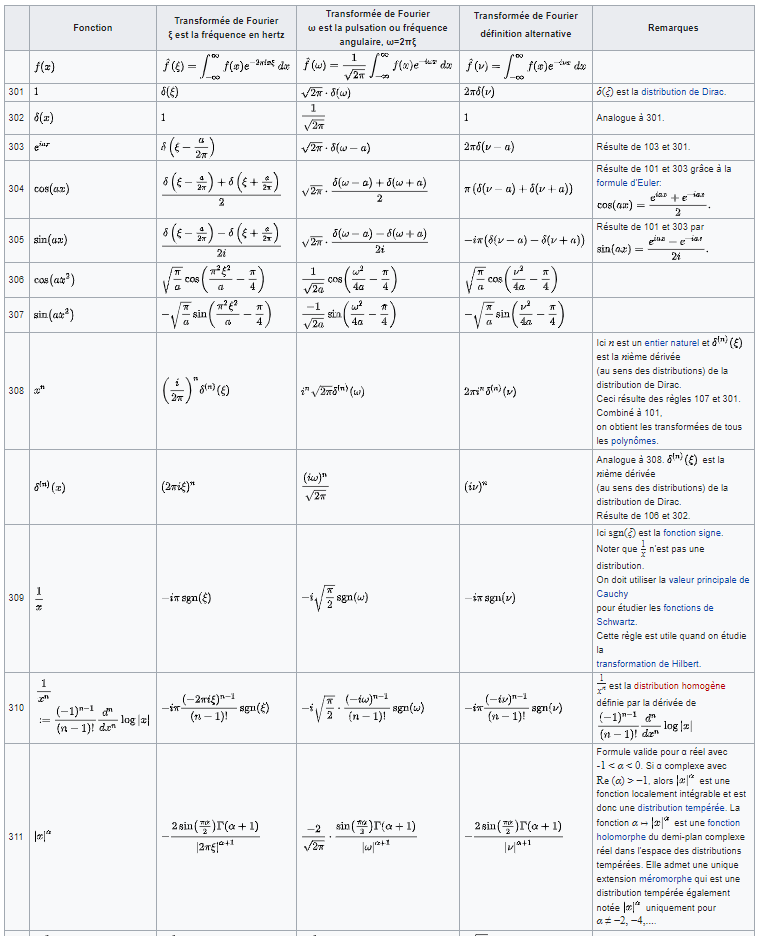
Transformations usuelles
A partir de la définition de la transformation, et des propriétés associées, les transformées de multiples fonctions ont été établies, formant ainsi des bibliothèque utiles dans divers domaines.
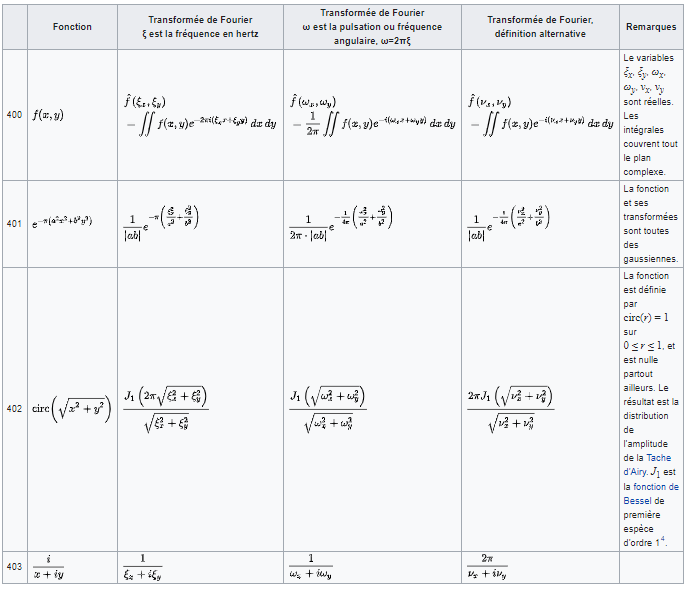
Des tableaux présentent les Transformations de FOURIER de certaines fonctions. Elles sont notées respectivement f̂, ĝ et ĥ, (n'apparaissent que les trois conventions les plus courantes). [WikiPédia]
• Fonctions à 1 variable: Ces transformées sont traitées dans Arthur Erdélyi, Tables of Integral Transforms, Vol. 1, McGraw-Hill, 1954, ou David Kammler, A First Course in Fourier Analysis, USA, Prentice Hall, 2000.
• Fonctions de carré intégrable à 1 variable: Ces transformées peuvent être trouvées dans les références précédentes ou dans George Campbell, Ronald Foster, Fourier Integrals for Practical Applications, New York, USA, D. Van Nostrand Company, Inc, 1948.
• Distributions à une variable: Ces transformées sont traitées dans Arthur Erdélyi, Tables of Integral Transforms, Vol. 1, McGraw-Hill, 1954 ou dans David Kammler, A First Course in Fourier Analysis, USA, Prentice Hall, 2000.
• Fonctions de deux variables: idem.
Transformations inverses
Aprés résolution dans l'espace de Fourier, les fonctions solutions doivent être retransformées pour avoir leurs expressions dans l'espace temporel initial:
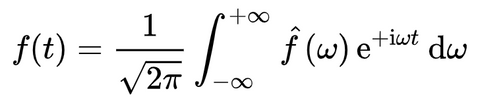
Transformations Inverses usuelles
La motivation est centrée sur le fait qu'à partir d'une transformée de FOURIER, on voudrait retrouver la fonction originale. L'objectif est :
• Trouver un bon candidat.
• Trouver un espace invariant.
• Continuité et inversion.
Transformations et signaux
Pour la plupart des fonctions rencontrées en physique, la transformée de Fourier de f existe :
• Train d'ondes: considérons un train d’onde sinusoïdal passant en un point M de l’espace (une onde de gravitation dans un fluide, une onde électromagnétique, une onde acoustique dans un tube, etc.). Le train d’onde sera décrit par une fonction "cosinus", dont la transformation est calculable.
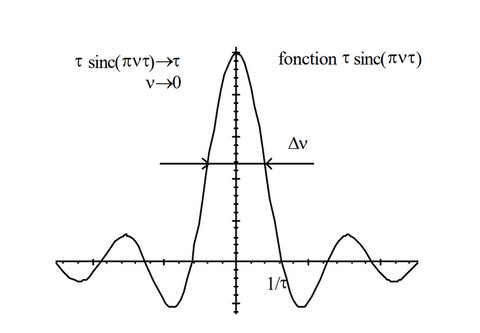
• Impulsion: Un autre exemple significatif est celui d’une impulsion rectangulaire de largeur t où le phénomène physique est représenté par la fonction « crénaux ».
• Impulsion: Un autre exemple significatif est celui d’une impulsion rectangulaire de largeur t où le phénomène physique est représenté par la fonction « crénaux ».
Jean Baptiste Joseph FOURIER

Jean Baptiste Joseph FOURIER est un mathématicien et physicien français né le 21 mars 1768 à Auxerre et mort le 16 mai 1830 à Paris (et non le 16 mars comme indiqué par erreur sur la plaque de bronze apposée sur sa maison natale) [Wikipédia].
• Théorie analytique de la chaleur et séries de Fourier: modélisation de l'évolution de la température au travers de séries trigonométriques.
• Effet de serre: l'un des premiers à avoir proposé, en 1824, une théorie selon laquelle les gaz de l'atmosphère terrestre augmentent la température à sa surface.
• Étude des systèmes d'inégalités et programmation linéaire: oui, c'est bien George DANTZIG qui a invente la programmation linéaire (dite aussi « optimisation linéaire »), mais avec une paternité plus lointaine qui en revient incontestablement à Joseph FOURIER.