Circuit RLC (série)
Schéma électrique
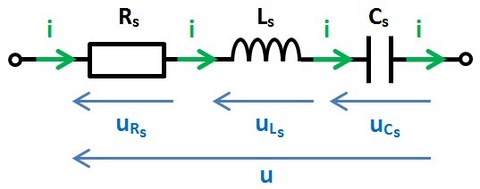
Le circuit est composé d'une résistance (RS), d'une inductance (LS) et d'un condensateur (CS). Les dipoles sont montés en série, et soumis à une tension u:
• Tensions: u = uR + uL + uC
• Intensités: i = iR = iL = IC
• Intensités: i = iR = iL = IC
La tension est égale à la somme des tension, alors que les courants sont tous identiques.
Impédance équivalente

L'impédance équivalente est égale à la somme des impédances complexes, soit:
• Z = R + j . L.(2πf) + 1 / [j.C.(2πf))]
• Z = R + j . [ L.(2πf) - 1 / C.(2πf) ]
• Z = R + j . [ L.(2πf) - 1 / C.(2πf) ]
Les expressions des calculs peuvent se simplifier en prennant en compte la pulsation (ώ=2πf) et des réactances inductives (XL=L.ώ) et capacitives (XC=1 / C.ώ):
• Z = R + j . [ L.ώ - 1 / C.ώ) ]
• Z = R + j . [ XL - XC) ]
• |Z| = √ [ R² + (XL - XC)² ]
• tan(ɸ) = (XL - XC) / R
• |Z| = √ [ R² + (XL - XC)² ]
• tan(ɸ) = (XL - XC) / R
Equation différencielle
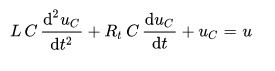
La tension est égale à la somme des tension :
• uR = R . i(t)
• uL = L . di(t)/dt
• uC = ∑ (1/C . i(t) . dt), suite i(t) = C.duC/dt depuis q=C.uC avec i=q/t
En définitive:
• u = [R . i] + [L . di/dt] + [∑ (1/C . i . dt)]
• i = (C . duC / dt)
• u = [R.C . duC / dt] + [L . d(C . duC / dt) / dt] + [∑ (1/C . (C . duC / dt) . dt)]
Au final:
Au final:
• u = [R.C . duC / dt] + [L.C . ( d²uC / dt²)] + [ uC]
C'est une équation différencielle du second ordre à coéficients constants.
Analyse temporelle
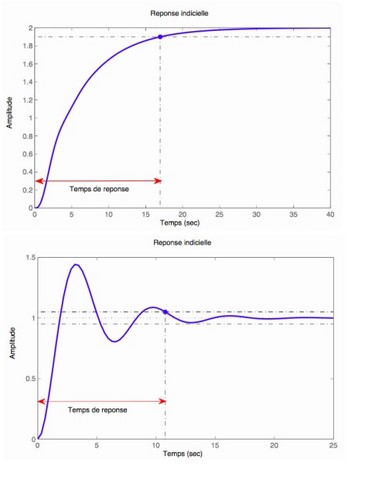
La solution de l'équation différencielle est la somme de la solution de l’équation homogène (régime libre) et d’une solution particulière (régime établi):
• régime libre: u(t) = A . e(r.t) ( plusieurs solutions suivant les paramêtres R, L, C, f).
• régime établi: Ze(t) = E (réponse à un échelon).
Pour simplifier les résultats, on défini diverses expressions (variables réduites):
• pulsation propre: ώ0 = 1 / √ (LC)
• facteur d'amortissement: λ = R / 2L.
• facteur d'amortissement: λ = R / 2L.
• coefficient d'amortissement: α = λ / ώ0.
• facteur de qualité: Q = 1 / 2α = L.ώ0 / R = 1 / RC.ώ0.
Les solutions de l'équation différencielle sont alors:
• régime apériodique: Q < 50%
→ racines du polynome: r 1/2= -λ ± √ (λ² - ώ²0)
→ constante: A1 = +r2.E / (r2 - r1)
→ constante: A2 = -r1.E / (r2 - r1)
→ solution: u(t) = A1.e(r1.t) + A2.e(r2.t)
• régime critique: Q = 50%
→ racine du polynome: r = -λ = -ώ²0
→ constante: A1 = λ.E
→ constante: A2 = E
→ solution: u(t) = (A1.t + A2).e(r2.t)
• régime pseudo-périodique: Q > 50%
→ racine du polynome: r1/2 = -λ ± jώ avec ώ=2π/T soit ώ=2π / [ώ0.√ (1-α²)]
→ constante: A1 = E
→ constante: A2 = (λ/ώ).E
→ solution: u(t) = [A1.cos(ώt) + A2.sin(ώt)] . e-λt
→ constante: A2 = E
→ solution: u(t) = (A1.t + A2).e(r2.t)
• régime pseudo-périodique: Q > 50%
→ racine du polynome: r1/2 = -λ ± jώ avec ώ=2π/T soit ώ=2π / [ώ0.√ (1-α²)]
→ constante: A1 = E
→ constante: A2 = (λ/ώ).E
→ solution: u(t) = [A1.cos(ώt) + A2.sin(ώt)] . e-λt
Analyse fréquencielle
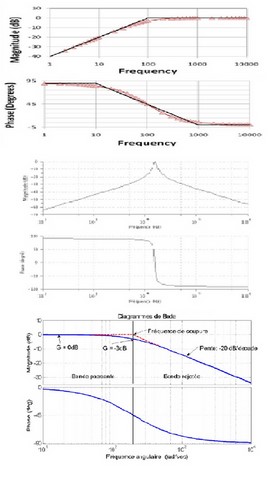
La réponse (en régime permanent) à un signal sinusoidal de fréquence variable u(t), s'observe au niveau des tensions aux bornes de la résistance (uR), de l'inductance (uL) et du condensateur (uC). En fait c'est chaque fois un quadripole de type pont diviseur de tension, de fonction de transfert H:
• résistance: HR = (ZR / ZRLC)
• inductance: HL = (ZL / ZRLC)
• condensateur: HC = (ZC / ZRLC)
Expressions remarquables:
• variables réduites:
→ pulsation propre: ώ0² = 1/LC
→ facteur: 2m = R / √ (LC)
→ facteur de Qualité: Q = 1/(2m) = (1/R) . √ (L/C)
Expressions remarquables:
• variables réduites:
→ pulsation propre: ώ0² = 1/LC
→ facteur: 2m = R / √ (LC)
→ facteur de Qualité: Q = 1/(2m) = (1/R) . √ (L/C)
→ Pulsation de coupure (RC): ώC = 1/RC
→ Pulsation de coupure (RL): ώC = R/L
Analyse aux bornes de la résistance (R):
Analyse aux bornes de la résistance (R):
• fonction de transfert:
→ expression générale: HR = (R) / [ (R) + (jLώ) + (1/jCώ) ]
→ expression générale: HR = (R) / [ (R) + (jLώ) + (1/jCώ) ]
→ expression réduite: HR = (j2m) / [1 + (j2m) . (ώ/ώ0) + (j.ώ/ώ0)²]
→ module: |HR| =
→ argument: Arg(HR) =
Analyse aux bornes de l'inductance (L):
• fonction de transfert:
→ expression générale: HL = (jLώ) / [ (R) + (jLώ) + (1/jCώ) ]
→ expression réduite: HL = j(ώ/ώC) / [ 1 + j(ώ/ώC) ]
→ module: |HL| = (ώ/ώC) / √ (1 + (ώ/ώC)² )
→ argument: Arg(HL) = (π/2) - arctan(ώ/ώC)
Analyse aux bornes du condensateur (C):
• fonction de transfert:
→ expression générale: HC = (1/jώ) / [ (R) + (jLώ) + (1/jCώ) ]
→ expression réduite: HC = 1 / [ 1 + j(ώ/ώC) ]
→ module: |HC| = 1 / √ (1 + (ώ/ώC)² )
→ argument: Arg(HC) = arctan(ώ/ώC)
• fonction de transfert:
→ expression générale: HL = (jLώ) / [ (R) + (jLώ) + (1/jCώ) ]
→ expression réduite: HL = j(ώ/ώC) / [ 1 + j(ώ/ώC) ]
→ module: |HL| = (ώ/ώC) / √ (1 + (ώ/ώC)² )
→ argument: Arg(HL) = (π/2) - arctan(ώ/ώC)
Analyse aux bornes du condensateur (C):
• fonction de transfert:
→ expression générale: HC = (1/jώ) / [ (R) + (jLώ) + (1/jCώ) ]
→ expression réduite: HC = 1 / [ 1 + j(ώ/ώC) ]
→ module: |HC| = 1 / √ (1 + (ώ/ώC)² )
→ argument: Arg(HC) = arctan(ώ/ώC)
→ gain: GdB = -10. log[1+(ώRC)²]
Analyse canonique:
• fonction de transfert:
→ pulsation réduite: u = ώ/ώ0
→ expression réduite: Hju = 1 / [1 + jQ.(u + (1/u)]
→ module: |Hju| = 1 / √ (1 + Q².(u-1/u)² )
→ argument: Arg(Hju) = arctan[Q.(u-1/u)]
→ gain: GdB = -10. log[]