Signaux
Définitions
DEFINITION MATHEMATIQUE
Un signal « s » est une application d'un ensemble « T » vers un ensemble « S » ou à toute variable « t » de « T » est associée une valeur « s(t) » de « S »:
s: T ---> St |---> s(t)
Si T est l'ensemble des réél (R), le signal s(t) est continu (analogique).
Si T est l'ensemble des entiers (N), le signal s(t) est discontinu (numérique)
MONOVARIABLES ET VECTORIEL
Dans le cas ou S est égal à R, ensemble des réels, les signaux S sont dits à « temps continu ». Le signal s(t) est un scalaire, et donc monovariable.
Si S est égal à Rn, le signal est une matrice, et donc vectoriel.
Dans le cas ou T est égal à Z, ensemble des entiers, les signaux S sont dits à « temps discrêt ».
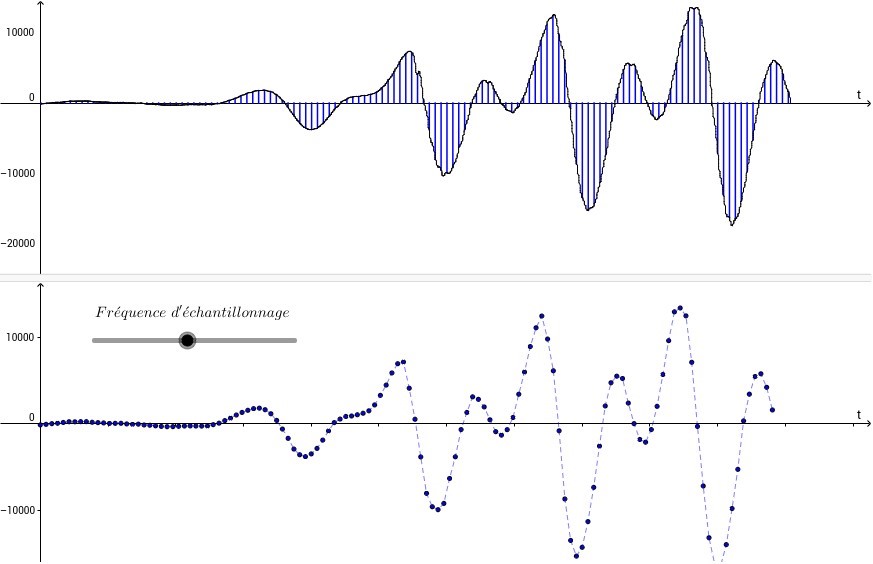
NUMERISATION ET ECHANTILLONNAGE
On défini par ST l'ensemble des applications de T dans S. Le signal s*(t) constitue alors le signal échantillonné. La durée entre deux instants successifs représente la période d'échantillonnage.
Le signal analogique s(t) peut être échantillonné à la période T pour donner s*(t), qui se transforme en un signal numérique b(n), après Conversion Analogique Numérique (CAN).
Le signal numérique b(n) peut être reconstitué en un signal analogique s(t) après Conversion Numérique Analogique (CNA) et mise en forme.
Signaux à temps continu types
FONCTION DE DIRAC
La fonction de DIRAC, dite impulsion, notée δ(t), est nulle pour tout instant t non nul, et infinie pour l'instant t0=0.
L'énergie du signal de Dirac est finie et unitaire, soit: ∫∞ δ(t) . dt = 0
FONCTION DE HEAVISIDE
La fonction de HEAVISIDE, dite échelon, est proportionnelle pour tout instant t.
C'est une rampe de pente constante, mais nulle pour les temps négatifs.
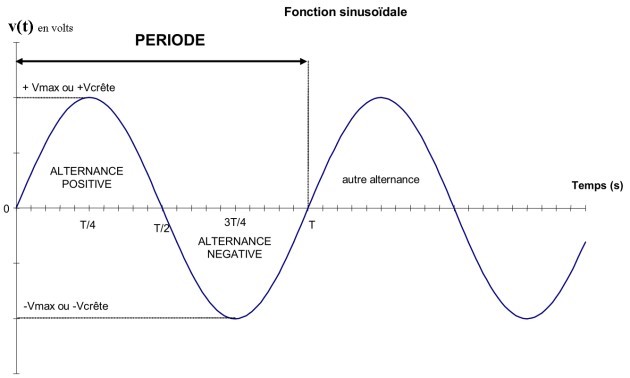
FONCTION SINUSOIDALE
La fonction sinusoidale est de type sinus ou cosinus, périodique de période T, et de valeur maximale (amplitude) Smax.
La phase à l'origine φ0 défini l'équation dans le temps: s(t) = Smax . sin(2π.t/T + φ0)